Zahlensysteme

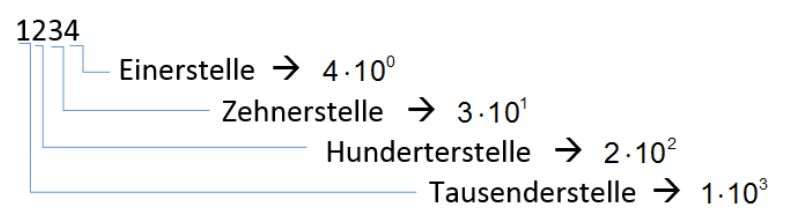
In einem Stellenwertsystem hat jede Stelle einen Wert. Er beträgt:

Basis^{Stellenposition, bei 0 beginnend}

Bsp (Dezimal): 10² = 100 (3 Stellen -> 0 1 2)
Bsp (Binär): 2⁷ = 1000 0000 (8 Stellen -> 0 1 2 3 4 5 6 7)

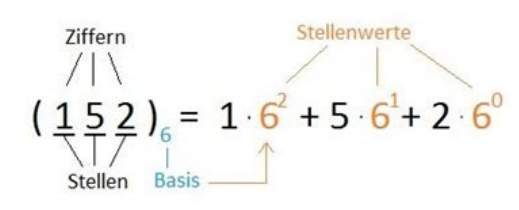
Stellenwertsystem	Basis	Ziffern
Dezimalsystem	10	0-9
Binärsystem	2	0-1
Oktalsystem	8	0-7
Hexadezimalsystem	16	0-9, A-F

20	21	22	23	24	25	26	27	28
1	2	4	8	16	32	64	128	256
29	210	211	212	213	214	215	216	217
512	1024	2056	4096	8192	16384	32768	65536	131072

Binär zu Dezimal

1	1	0	1	0	0	1	0	Binär
1 x 27	1 x 26	0 x 25	1 x 24	0 x 23	0 x 22	1 x 21	0 x 20	Summe
128	64	0	16	0	0	2	0	= 210

Binär zu Hexadecimal

• Binärzahl in 4er Blöcke aufteilen.
• Fehlende Nullen beim vordersten Block auffüllen und mit unten stehender Tabelle umrechnen
• Die Umrechnung Hexadecimal zu Binär erfolgt analog nur umgekehrt

Hex	Binär	Hex	Binär
0	0000	8	1000
1	0001	9	1001
2	0010	A	1010
3	0011	B	1011
4	0100	C	1100
5	0101	D	1101
6	0110	E	1110
7	0111	F	1111

Dezimal zu Binär

Das Ergebnis wird von unten nach oben gelesen!

94 / 2 = 47 Rest 0  ^
47 / 2 = 23 Rest 1  ^
23 / 2 = 11 Rest 1  ^
11 / 2 = 5  Rest 1  ^
5  / 2 = 2  Rest 1  ^
2  / 2 = 1  Rest 0  ^
1  / 2 = 0  Rest 1  ^

= 1011110

Dezimal zu Hexadezimal

1. Dezimal zu Binär umrechnen
2. Binärzahl in 4er Blöcke einteilen und fehlende Nullen auffüllen
3. Die 4er Blöcke zu Hexadezimalzahlen umrechnen (siehe Tabelle)

Hexadezimal zu Dezimal

2	A	5	E	Hexadecimal
2 x 163	10 x 162	5 x 161	14 x 160	Summe
8192	2560	80	14	= 10846

Binäre Arithmetik

1. Binäres Addieren
   (z. B.: 1010 + 0101)

   • Stelle 1: 0 + 1 = 1 von rechts
   • Stelle 2: 1 + 0 = 1
   • Stelle 3: 0 + 1 = 1
   • Stelle 4: 1 + 0 = 1

   =========================
   Ergebnis: 1111

   (Hinweis: Bei 1+1 schreibt man 0 und überträgt 1.)

2. Binäres Subtrahieren
   (z. B.: 1010 - 0101)

   • Stelle 1: 0 - 1 → nicht möglich, also leihen => 10₂ - 1 = 1; nächst höhere Stelle wird um 1 reduziert.
   • Stelle 2: (1-1) = 0 (wegen Leihen)
   • Stelle 3: 0 - 1 → wieder leihen => 10₂ - 1 = 1; nächst höhere Stelle um 1 reduziert.
   • Stelle 4: (1-1) = 0

   =========================
   Ergebnis: 0101

   (Hinweis: Leihen im Binärsystem entspricht dem Hinzufügen von 2.)

3. Bitweise Operationen
   (Bit-für-Bit, bei gleicher Stellenzahl):

   a) AND:

      - Regel: Nur 1, wenn beide Bits 1 sind; sonst 0.

        1010  
      & 0101 
      = 0000  

   b) OR:

      Regel: 1, wenn mindestens ein Bit 1 ist.

        1010 
      | 0101 
      = 1111

   c) XOR:

      Regel: 1, wenn die Bits unterschiedlich sind; sonst 0.

      1010 
    ^ 0101 
    = 1111